मात्रात्मक अर्थशास्त्र वित्तीय प्रणालियों की मापने योग्य विशेषताओं को देखता है
Contents
- 1 Module 1:
- 2 Module 2:
- 3 Module 3:
- 4 Module 4:
- 4.0.1 समय श्रृंखला
- 4.0.2 काल श्रेणी के अंग
- 4.0.3 दीर्घकालीन प्रवृति का मापन (Measurement of trend)
- 4.0.3.1 . स्वतंत्र हस्तवक्र या बिन्दुरेखीय रीति (Freehand curve of Graphic method)
- 4.0.3.2 2. अर्द्ध-माध्य रीति (Semi-Average Method) –
- 4.0.3.3 3. चल-माध्य रीति (Moving Average Method)
- 4.0.3.4 4. न्यूनतम वर्ग रीति (Method of Least Squares)
- 4.0.3.5 5. अर्द्ध-लघुगणकीय या घातांकीय वक्र (Semi logarithmic of Expontial curve)
- 4.0.4 मौसमी परिवर्तन मापन की विधि (Measurement of Seasonal Variations)
- 5 Module 5:
- 5.0.1 सूचकांक संख्या
- 5.0.2 📌 1. संख्यात्मक विधियाँ (Statistical Techniques)
- 5.0.3 1.1 औसत (Mean)
- 5.0.4 1.2 माध्य विचलन (Measures of Dispersion)
- 5.0.5 1.3 सहसंबंध और प्रतिगमन (Correlation & Regression)
- 5.0.6 📐 2. वस्तु नाभिक (Index Numbers)
- 5.0.7 🧮 3. समय-श्रृंखला विधियाँ (Time Series Methods)
- 5.0.8 🧮 4. संभावना (Probability Basics)
- 5.0.9 🧾 5. आर्थिक अनुप्रयोग (Economic Applications)
- 5.0.10 📈 6. उपलब्ध व्यक्ति (Useful Formulae Summary)
- 5.0.11 ⏱️ Examination Strategies
- 5.0.12 📥 यदि आप चाहें तो:
- 5.0.13 B.A Part 3 Paper 6 : QUANTITATIVE TECHNIQUES(मात्रात्मक तकनीकें) | Economics Short Notes for TMBU Bhagalpur
- 5.0.14 Evaluation of In-vitro Rheumatoid Arthritic Activity of …
Module 1:
| Module 1: Introduction to statistics Basic concept population sample parameter frequency distribution cumulative frequency graphics and diagrammatic representation of data techniques of Data Collection sampling versus population primary and secondary data |
मॉड्यूल 1: सांख्यिकी का परिचय मूल अवधारणा जनसंख्या नमूना पैरामीटर आवृति वितरण संचयी आवृत्ति डेटा संग्रह की डेटा तकनीकों का ग्राफिक्स और आरेखीय प्रतिनिधित्व नमूनाकरण बनाम जनसंख्या प्राथमिक और द्वितीयक डेटा |
जनगणना जनसंख्या के प्रत्येक सदस्य से डेटा एकत्र करने की प्रक्रिया है, जबकि नमूना जनसंख्या के एक सबसेट से डेटा एकत्र करने की प्रक्रिया है। एक जनगणना में, जनसंख्या के प्रत्येक सदस्य को शामिल किया जाता है, जबकि नमूने में, व्यक्तियों के एक छोटे समूह को समग्र रूप से जनसंख्या का प्रतिनिधित्व करने के लिए चुना जाता है।
| जनगणना | सैम्पलिंग |
| जनसंख्या के प्रत्येक सदस्य से डेटा एकत्र करना शामिल है | एक सबसेट या आबादी के एक चयनित समूह से डेटा एकत्र करना शामिल है |
| सर्वेक्षण करने और डेटा एकत्र करने के लिए बड़ी मात्रा में संसाधनों और समय की आवश्यकता होती है | कम संसाधनों की आवश्यकता होती है और यह आचरण करने में तेज होता है क्योंकि इसमें केवल जनसंख्या का एक विशिष्ट समूह शामिल होता है |
| जनसंख्या का पूर्ण और सटीक प्रतिनिधित्व प्रदान करता है क्योंकि इसमें सभी सदस्य शामिल होते हैं | चयनित नमूने के आधार पर जनसंख्या का अनुमान या सामान्य विचार प्रदान करता है |
| नमूनाकरण की तुलना में अधिक महंगा हो सकता है क्योंकि इसमें जनसंख्या के प्रत्येक सदस्य से डेटा एकत्र करना शामिल है | आम तौर पर जनगणना की तुलना में कम खर्चीला होता है क्योंकि इसमें केवल जनसंख्या का एक विशिष्ट समूह शामिल होता है |
| छोटी आबादी के लिए उपयोगी हो सकता है या जब पूरी आबादी के बारे में विस्तृत जानकारी की आवश्यकता हो | बड़ी आबादी के लिए उपयोगी हो सकता है या जब जनसंख्या के बारे में सामान्य अवलोकन की आवश्यकता होती है |
| त्रुटि का मार्जिन आम तौर पर बहुत छोटा होता है क्योंकि यह पूरी आबादी को कवर करता है | त्रुटि का मार्जिन आम तौर पर जनगणना से बड़ा होता है क्योंकि नमूना आकार जनसंख्या के आकार से छोटा होता है |
जनगणना और नमूनाकरण के बीच मुख्य अंतर
- जनगणना जनसंख्या के प्रत्येक सदस्य से डेटा एकत्र करने की प्रक्रिया है, जबकि नमूनाकरण जनसंख्या से व्यक्तियों के एक सबसेट का चयन करने की प्रक्रिया है जो संपूर्ण का प्रतिनिधित्व करता है।
- जनगणना के आंकड़े नमूने के आंकड़ों की तुलना में अधिक सटीक और सटीक होते हैं, क्योंकि इसमें जनसंख्या के प्रत्येक सदस्य की जानकारी शामिल होती है।
- जनगणना डेटा संग्रह आम तौर पर अधिक समय लेने वाला और नमूना लेने की तुलना में महंगा होता है, क्योंकि इसके लिए जनसंख्या में प्रत्येक व्यक्ति तक पहुंचने की आवश्यकता होती है।
- नमूनाकरण डेटा संग्रह का एक अधिक कुशल तरीका है और छोटे नमूना आकार के साथ जनसंख्या का अच्छा प्रतिनिधित्व प्रदान कर सकता है।
- जनगणना आमतौर पर एक पूरे देश के लिए की जाती है जबकि नमूना अध्ययन और अनुसंधान के लिए उपयोग किया जाता है, यह एक विशिष्ट क्षेत्र या लोगों के समूह के लिए भी किया जा सकता है।
जनगणना पर अवलोकन
जनगणना एक जनसंख्या की गणना और विवरण है, जो आम तौर पर एक सरकार द्वारा आयोजित की जाती है। जनगणना में एकत्र की गई जानकारी का उपयोग विभिन्न उद्देश्यों के लिए किया जा सकता है, जैसे सरकारी धन आवंटित करना और विधायी निकाय में सीटों की संख्या निर्धारित करना। जनगणना आमतौर पर हर 10 साल में की जाती है। जनगणना में एकत्र की गई जानकारी में जनसांख्यिकीय जानकारी शामिल हो सकती है, जैसे आयु, लिंग, जाति और आय, साथ ही आवास और रोजगार के बारे में जानकारी। जनसंख्या की जरूरतों को समझने और योजना बनाने के लिए जनगणना एक महत्वपूर्ण उपकरण है।
जनगणना के फायदे और नुकसान
जनगणना के लाभ:-
- जनसंख्या की व्यापक तस्वीर प्रदान करता है: जनगणना डेटा जनसंख्या की जनसांख्यिकीय, सामाजिक और आर्थिक विशेषताओं के बारे में विस्तृत जानकारी प्रदान करता है, जिसका उपयोग सार्वजनिक नीति और नियोजन निर्णयों को सूचित करने के लिए किया जा सकता है।
- आवश्यकता के क्षेत्रों की पहचान करने में मदद करता है: जनगणना डेटा का उपयोग उच्च गरीबी, निम्न शैक्षिक प्राप्ति, या आवश्यकता के अन्य संकेतकों के क्षेत्रों की पहचान करने के लिए किया जा सकता है, जिन्हें सरकारी सहायता या अन्य कार्यक्रमों के लिए लक्षित किया जा सकता है।
- विभाजन और पुनर्वितरण के लिए उपयोग किया जाता है:जनगणना के आंकड़ों का उपयोग राज्यों के बीच अमेरिकी प्रतिनिधि सभा में सीटों को विभाजित करने और राज्य और स्थानीय स्तरों पर विधायी जिलों को फिर से तैयार करने के लिए किया जाता है।
- संघीय निधियों के आवंटन के लिए उपयोग किया जाता है: जनगणना डेटा का उपयोग मेडिकेड, हेड स्टार्ट और राजमार्ग निर्माण जैसे कार्यक्रमों के लिए राज्य और स्थानीय सरकारों को संघीय निधियों में अरबों डॉलर वितरित करने के लिए किया जाता है।
- व्यवसायों को सूचित निर्णय लेने में मदद करता है: व्यवसाय संभावित बाजारों की पहचान करने के लिए जनगणना डेटा का उपयोग करते हैं, जहां पता लगाना है, और भविष्य के विकास की योजना बनाने के बारे में निर्णय लेने के लिए।
- शैक्षणिक अनुसंधान के लिए डेटा प्रदान करता है: जनसंख्या के रुझान, आर्थिक विकास और अन्य मुद्दों का अध्ययन करने के लिए जनगणना डेटा का उपयोग शोधकर्ताओं द्वारा विभिन्न प्रकार के क्षेत्रों में किया जाता है।
- नागरिक अधिकार प्रवर्तन की सुविधा: जनगणना डेटा का उपयोग उन कानूनों को लागू करने के लिए किया जाता है जो आवास, रोजगार और अन्य क्षेत्रों में भेदभाव को प्रतिबंधित करते हैं।
- निष्पक्ष राजनीतिक प्रतिनिधित्व सुनिश्चित करने में मदद करता है: जनगणना डेटा का उपयोग यह सुनिश्चित करने के लिए किया जाता है कि सभी समुदायों को सरकार में उचित प्रतिनिधित्व मिले। यह सुनिश्चित करता है कि सभी आवाजें सुनी जाएं और यह कि सभी समुदायों का शासन में समान अधिकार है।
जनगणना के नुकसान:-
- उच्च लागत: जनगणना आयोजित करना एक महंगा प्रयास हो सकता है, जिसके लिए कर्मियों, प्रौद्योगिकी और बुनियादी ढांचे में महत्वपूर्ण निवेश की आवश्यकता होती है।
- गोपनीयता संबंधी चिंताएँ: कुछ व्यक्ति इस डर से सरकार को व्यक्तिगत जानकारी प्रदान करने में हिचकिचा सकते हैं कि अनधिकृत पार्टियों द्वारा इसका दुरुपयोग या उपयोग किया जा सकता है।
- सीमित सटीकता: जनगणना डेटा स्व-रिपोर्ट की गई जानकारी पर निर्भर करता है, जो हमेशा सटीक या पूर्ण नहीं हो सकता है। इसके अतिरिक्त, भाषा बाधाओं, सरकार के प्रति अविश्वास, या गतिशीलता जैसे कारकों के कारण कुछ व्यक्ति जनगणना से छूट सकते हैं।
- सीमित दायरा: एक जनगणना केवल एक विशिष्ट समय पर आबादी का एक स्नैपशॉट प्रदान कर सकती है, और जनगणना के बीच होने वाले महत्वपूर्ण रुझानों या परिवर्तनों को पकड़ने में सक्षम नहीं हो सकती है।
- कुछ आबादी को कम आंकता है: कुछ जनसंख्या समूहों को ऐतिहासिक रूप से गिनना कठिन होता है, जैसे कि बेघर, प्रवासी और बिना कानूनी स्थिति वाले लोग। नतीजतन, इन आबादी को जनगणना में कम गिना जा सकता है, जिससे डेटा में गलतियां हो सकती हैं।
- लचीलेपन की कमी: जनगणना डेटा निर्धारित अंतराल (आमतौर पर हर 10 साल) पर एकत्र किया जाता है और बदलती परिस्थितियों के लिए पर्याप्त रूप से प्रतिक्रिया देने में सक्षम नहीं हो सकता है।
- अनुवर्ती कार्रवाई के लिए सीमित क्षमता: जनगणना डेटा कुछ विषयों के बारे में विस्तृत जानकारी प्रदान नहीं कर सकता है, और समय, बजट और राजनीतिक बाधाओं के कारण अनुवर्ती सर्वेक्षण संभव नहीं हो सकता है।
- सीमित तुलनात्मकता: परिभाषाओं, वर्गीकरणों और अन्य कारकों में अंतर के कारण विभिन्न देशों या क्षेत्रों के जनगणना डेटा की सीधे तुलना नहीं की जा सकती है।
नमूनाकरण पर अवलोकन
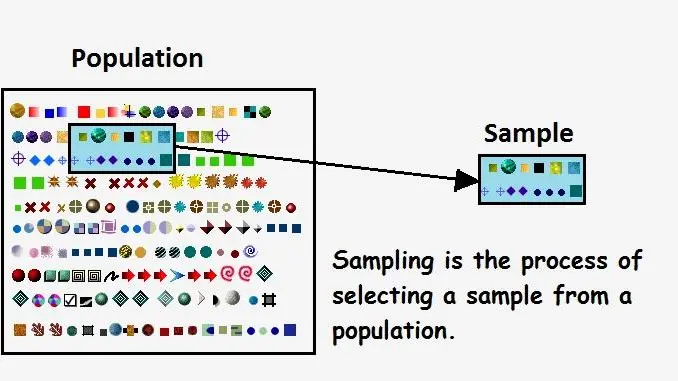
नमूनाकरण पूरी आबादी की विशेषताओं का अनुमान लगाने के लिए एक बड़ी आबादी से टिप्पणियों के सबसेट का चयन करने की प्रक्रिया है। प्रेक्षणों का सबसेट, या नमूना, एक विशिष्ट विधि का उपयोग करके चुना जाता है, जैसे यादृच्छिक नमूनाकरण, पूर्वाग्रह को कम करने के लिए और इस संभावना को बढ़ाने के लिए कि नमूना सटीक रूप से जनसंख्या का प्रतिनिधित्व करता है। नमूनाकरण का उपयोग सांख्यिकी, अनुसंधान और डेटा विश्लेषण सहित विभिन्न क्षेत्रों में किया जाता है, और यह सीमित डेटा के आधार पर आबादी के बारे में अनुमान लगाने के लिए एक महत्वपूर्ण उपकरण है।
सैंपलिंग के फायदे और नुकसान
प्रतिचयन के लाभ:-
- कम डेटा आवश्यकताएँ: नमूनाकरण संपूर्ण डेटासेट के बजाय डेटा के एक छोटे, प्रतिनिधि सबसेट के विश्लेषण की अनुमति देता है, कम्प्यूटेशनल और भंडारण आवश्यकताओं को कम करता है।
- दक्षता में वृद्धि:नमूनाकरण डेटा विश्लेषण की दक्षता में काफी वृद्धि कर सकता है, जिससे तेजी से और अधिक लागत प्रभावी निष्कर्ष निकाले जा सकते हैं।
- बेहतर प्रतिनिधित्व: नमूनाकरण यह सुनिश्चित कर सकता है कि विश्लेषण के लिए उपयोग किए जाने वाले डेटा का सबसेट संपूर्ण डेटासेट का अधिक प्रतिनिधि है, जिससे अधिक सटीक और विश्वसनीय निष्कर्ष निकलते हैं।
- डेटा का सरलीकरण: नमूनाकरण जटिल डेटा सेट को सरल बना सकता है और उन्हें विश्लेषण के लिए अधिक प्रबंधनीय बना सकता है।
- पैटर्न की पहचान: बड़े डेटा सेट में पैटर्न और प्रवृत्तियों की पहचान करने के लिए नमूनाकरण का उपयोग किया जा सकता है जो पूरे डेटासेट का विश्लेषण करते समय स्पष्ट नहीं हो सकता है।
- लागत प्रभावी: संपूर्ण डेटासेट का विश्लेषण करने की तुलना में नमूनाकरण अक्सर कम खर्चीला और समय लेने वाला होता है, जिससे यह सीमित संसाधनों वाले संगठनों के लिए एक आकर्षक विकल्प बन जाता है।
- सामान्यीकरण में सुधार: नमूनाकरण से जनसंख्या के निष्कर्षों का बेहतर सामान्यीकरण हो सकता है, क्योंकि नमूना जनसंख्या का एक प्रतिनिधि उपसमुच्चय है।
सैंपलिंग के नुकसान:-
- नमूनाकरण त्रुटि: नमूनाकरण त्रुटि की संभावना, या नमूना और जनसंख्या आंकड़ों के बीच का अंतर, गलत निष्कर्ष और अविश्वसनीय परिणाम दे सकता है।
- पूर्वाग्रह: नमूनाकरण विधियाँ जो ठीक से क्रियान्वित नहीं की जाती हैं, नमूने में पूर्वाग्रह का परिचय दे सकती हैं, जिससे जनसंख्या के बारे में गलत निष्कर्ष निकल सकते हैं।
- सीमित सामान्यता: जबकि नमूनाकरण सामान्यता में सुधार कर सकता है, यह इसे सीमित भी कर सकता है यदि नमूना जनसंख्या का प्रतिनिधि नहीं है।
- जटिलता: नमूनाकरण एक जटिल प्रक्रिया हो सकती है, जिसके लिए सांख्यिकीय विधियों और तकनीकों को सही ढंग से निष्पादित करने की पूरी समझ की आवश्यकता होती है।
- गुम डेटा: नमूनाकरण के परिणामस्वरूप लापता डेटा हो सकता है, जो परिणामों की वैधता और विश्वसनीयता को प्रभावित कर सकता है।
- छोटा नमूना आकार: एक छोटा नमूना आकार परिणामों में कम सटीकता और उच्च परिवर्तनशीलता का कारण बन सकता है, जिससे जनसंख्या के बारे में सटीक निष्कर्ष निकालना मुश्किल हो जाता है।
- जनसंख्या का अपर्याप्त ज्ञान: नमूनाकरण से गलत निष्कर्ष निकल सकते हैं यदि शोधकर्ता को अध्ययन की जा रही जनसंख्या का अपर्याप्त ज्ञान है।
जनगणना और नमूनाकरण के बीच समानताएं
- जनगणना और नमूनाकरण दोनों में जनसंख्या से डेटा का संग्रह शामिल है।
- दोनों विधियों में, प्रश्नों या चरों के पूर्वनिर्धारित सेट का उपयोग करके डेटा एकत्र किया जाता है।
- नमूने से एकत्र किए गए डेटा के आधार पर आबादी के बारे में अनुमान लगाने के लिए दोनों विधियों का उपयोग किया जाता है।
- दोनों विधियों में जनसंख्या के बारे में किए गए अनुमानों में त्रुटि का मार्जिन उत्पन्न करने की क्षमता है।
- एक नमूने का चयन करने या जनगणना करने के लिए दोनों विधियों के लिए एक नमूना फ्रेम, या जनसंख्या के सभी सदस्यों की एक सूची की आवश्यकता होती है।
- दोनों विधियों का उपयोग विभिन्न प्रकार के अनुसंधानों के लिए किया जा सकता है, जैसे मात्रात्मक या गुणात्मक अनुसंधान।
- दोनों विधियों का उपयोग विभिन्न क्षेत्रों में किया जा सकता है, जैसे बाजार अनुसंधान, सामाजिक विज्ञान अनुसंधान और आधिकारिक सांख्यिकी।
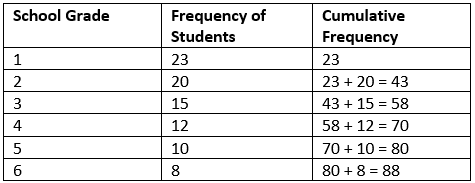
आवृति वितरण & संचयी आवृत्ति
जनसंख्या & नमूना
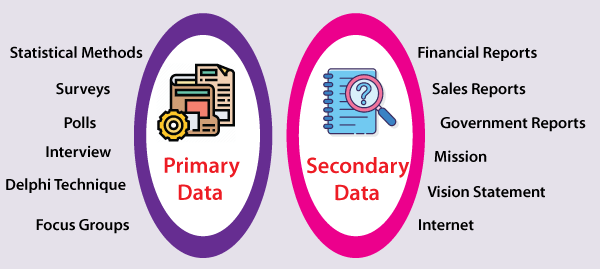
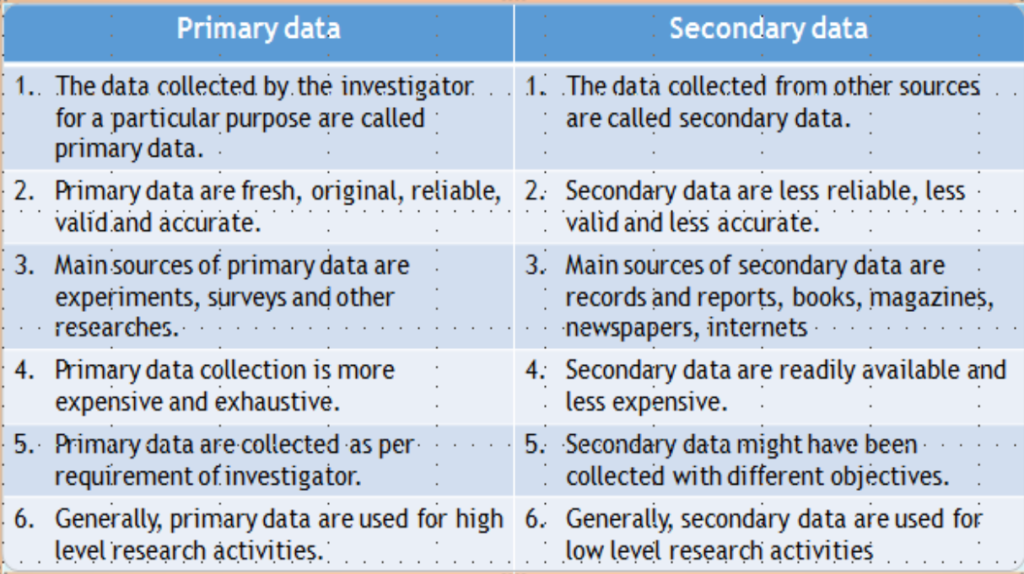
प्राथमिक और द्वितीयक डेटा
Module 2:
| Central tendency and dispersion measurement of Central tendency Mean Median Mode geometric mean and harmonic mean measures of dispersion – range, mean deviation, standard deviation coefficient of variation quartile deviation skewness and kurtosis |
केंद्रीय प्रवृत्ति एवं फैलाव केंद्रीय प्रवृत्ति माध्य माध्यिका मोड का मापन ज्यामितीय माध्य और हार्मोनिक माध्य फैलाव के माप – सीमा, माध्य विचलन, मानक विचलन गुणांक का परिवर्तन चतुर्थक विचलन तिरछापन और कुर्टोसिस |
केंद्रीय प्रवृत्ति
केन्द्रीय प्रवृत्ति की माप एक सारांश आँकड़ा है जो केन्द्र बिन्दु या किसी डाटासेट के विशिष्ट मान का प्रतिनिधित्व करता है। दूसरे शब्दों में कहा जाए तो केन्द्रीय प्रवृत्ति एक समंक श्रेणी के केंद्र में स्थित ऐसा मूल्य है, जिसके आस-पास आवृत्तियों के केन्द्रित होने की प्रवृत्ति होती है तथा जो श्रेणी के लक्षणों का प्रतिनिधित्व करता है। इसे सांख्यिकीय माध्य भी कहा जाता है। सांख्यिकी में केंद्रीय प्रवृत्ति का मापन तीन विधियों द्वारा किया जाता है-माध्य (Mean) , माध्यिका (Median) बहुलक (Mode) । यहाँ हम इन तीनों विधियों की क्रमबद्ध व्याख्या करेंगे।
Measures of Central Tendency
1. Mean: It is the average of all the values given in a set of data.
2. Mode: The mode is the number that appears most frequently in a set of data. We can find the mode by counting the number of times each value occurs in a data set.
3. Median: Median is the most middle value in a set of data. Let n denotes the number of observations in a data set. If n is odd, the median equals the [(n+1)/2]th observation.
If n is even, then the median is given by the mean of (n/2)th observation and [(n/2)+1]th Observation.
केंद्रीय प्रवृत्ति के माप
1. माध्य: यह डेटा के एक सेट में दिए गए सभी मानों का औसत है।
2. मोड : मोड वह संख्या है जो डेटा के सेट में सबसे अधिक बार दिखाई देती है। हम डेटा सेट में प्रत्येक मान के आने की संख्या की गणना करके मोड का पता लगा सकते हैं।
3. माध्यिका: माध्यिका डेटा के एक सेट में सबसे मध्य मान है। मान लीजिए n किसी डेटा सेट में अवलोकनों की संख्या को दर्शाता है। यदि n विषम है, तो माध्यिका [(n+1)/2] वें अवलोकन के बराबर है।
यदि n सम है, तो माध्यिका (n/2) वें अवलोकन और [(n/2)+1] वें के माध्यम से दी जाती है
अवलोकन।
Formula
1. Mean = [number of observations]/[total number of observations]
For grouped data, mean is:
2. Median for ungrouped data:
Median = [(n+1)/2]th observation, if n is odd.
Median = mean of (n/2)th observation and [(n/2)+1]th observation, if n is even.
Median for grouped data:
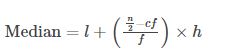
3. Mode: To find the mode, arrange the given data in the ascending order. Then count how many times each number is occurring. The number that occurs most, is the mode.

Estimating mode from grouped data: Find the group with the highest frequency (modal group).
Estimated mode = L +[(fm-fm-1)/(fm-fm-1)+(fm-fm+1)]×W
L denotes the lower class boundary of the modal group.
fm-1 denotes the frequency of the group before the modal group.
fm denotes the frequency of the modal group.
fm+1 denotes the frequency of the group after the modal group.
W denotes the group width.
1. माध्य = [अवलोकनों की संख्या]/[अवलोकनों की कुल संख्या]
समूहीकृत डेटा के लिए, माध्य है:
2. अवर्गीकृत डेटा के लिए माध्यिका:
माध्यिका = [(n+1)/2] वां अवलोकन, यदि n विषम है।
माध्यिका = (n/2) वें अवलोकन और [(n/2)+1] वें अवलोकन का माध्य, यदि n सम है।
समूहीकृत डेटा के लिए माध्यिका:
3. मोड: मोड खोजने के लिए दिए गए डेटा को आरोही क्रम में व्यवस्थित करें। फिर गिनें कि प्रत्येक संख्या कितनी बार घटित हो रही है। जो संख्या सबसे अधिक आती है, वह बहुलक है।
समूहीकृत डेटा से मोड का अनुमान लगाना: उच्चतम आवृत्ति (मोडल समूह) वाला समूह ढूंढें।
अनुमानित मोड = L +[(f m -f m-1 )/(f m -f m-1 )+(f m -f m+1 )]×W
L, मोडल समूह की निम्न वर्ग सीमा को दर्शाता है।
f m-1, मोडल समूह से पहले समूह की आवृत्ति को दर्शाता है।
f m मोडल समूह की आवृत्ति को दर्शाता है।
f m+1 मोडल समूह के बाद समूह की आवृत्ति को दर्शाता है।
W समूह की चौड़ाई को दर्शाता है।
फैलाव
आँकड़ों में , फैलाव (जिसे परिवर्तनशीलता , बिखराव या प्रसार भी कहा जाता है ) वह सीमा है जिस तक वितरण को बढ़ाया या निचोड़ा जाता है
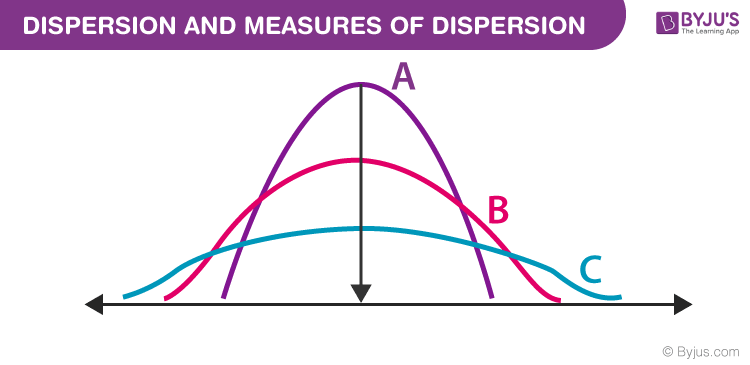
Types of Measures of Dispersion
There are two main types of dispersion methods in statistics which are:
- Absolute Measure of Dispersion
- Relative Measure of Dispersion
परिक्षेपण के माप के प्रकार
सांख्यिकी में प्रकीर्णन विधियाँ दो मुख्य प्रकार की होती हैं जो इस प्रकार हैं:
- फैलाव का पूर्ण माप
- फैलाव का सापेक्ष माप
Absolute Measure of Dispersion
An absolute measure of dispersion contains the same unit as the original data set. The absolute dispersion method expresses the variations in terms of the average of deviations of observations like standard or means deviations. It includes range, standard deviation, quartile deviation, etc.

4. मानक विचलन:
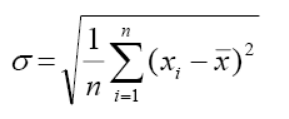
5. माध्य विचलन
समूहीकृत आवृत्ति वितरण के लिए,
6. रेंज = एल – एस
यहां एल विचाराधीन यादृच्छिक चर द्वारा प्राप्त अधिकतम मूल्य है और एस न्यूनतम मूल्य है।
7. चतुर्थक विचलन
The types of absolute measures of dispersion are:
- Range: It is simply the difference between the maximum value and the minimum value given in a data set. Example: 1, 3,5, 6, 7 => Range = 7 -1= 6
- Variance: Deduct the mean from each data in the set, square each of them and add each square and finally divide them by the total no of values in the data set to get the variance. Variance (σ2) = ∑(X−μ)2/N
- Standard Deviation: The square root of the variance is known as the standard deviation i.e. S.D. = √σ.
- Quartiles and Quartile Deviation: The quartiles are values that divide a list of numbers into quarters. The quartile deviation is half of the distance between the third and the first quartile.
- Mean and Mean Deviation: The average of numbers is known as the mean and the arithmetic mean of the absolute deviations of the observations from a measure of central tendency is known as the mean deviation (also called mean absolute deviation).
फैलाव का पूर्ण माप
फैलाव के एक पूर्ण माप में मूल डेटा सेट के समान ही इकाई होती है। पूर्ण विचरण विधि मानक या साधन विचलन जैसे अवलोकनों के विचलन के औसत के संदर्भ में भिन्नता को व्यक्त करती है। इसमें सीमा, मानक विचलन , चतुर्थक विचलन आदि शामिल हैं।
परिक्षेपण के निरपेक्ष माप के प्रकार हैं:
- रेंज: यह डेटा सेट में दिए गए अधिकतम मूल्य और न्यूनतम मूल्य के बीच का अंतर है। उदाहरण: 1, 3,5, 6, 7 => रेंज = 7 -1= 6
- भिन्नता: सेट में प्रत्येक डेटा से माध्य घटाएं, उनमें से प्रत्येक का वर्ग करें और प्रत्येक वर्ग को जोड़ें और अंत में भिन्नता प्राप्त करने के लिए उन्हें डेटा सेट में मानों की कुल संख्या से विभाजित करें। प्रसरण (σ 2 ) = ∑(X−μ) 2 /N
- मानक विचलन: विचरण के वर्गमूल को मानक विचलन यानी SD = √σ के रूप में जाना जाता है।
- चतुर्थक और चतुर्थक विचलन: चतुर्थक वे मान हैं जो संख्याओं की सूची को चतुर्थांश में विभाजित करते हैं। चतुर्थक विचलन तीसरे और पहले चतुर्थक के बीच की दूरी का आधा है।
- माध्य और माध्य विचलन: संख्याओं के औसत को माध्य के रूप में जाना जाता है और केंद्रीय प्रवृत्ति के माप से अवलोकनों के पूर्ण विचलन के अंकगणितीय माध्य को माध्य विचलन (जिसे माध्य निरपेक्ष विचलन भी कहा जाता है) के रूप में जाना जाता है।
Relative Measure of Dispersion
The relative measures of dispersion are used to compare the distribution of two or more data sets. This measure compares values without units. Common relative dispersion methods include:
- Co-efficient of Range
- Co-efficient of Variation
- Co-efficient of Standard Deviation
- Co-efficient of Quartile Deviation
- Co-efficient of Mean Deviation
Co-efficient of Dispersion
The coefficients of dispersion are calculated (along with the measure of dispersion) when two series are compared, that differ widely in their averages. The dispersion coefficient is also used when two series with different measurement units are compared. It is denoted as C.D.
The common coefficients of dispersion are:
| C.D. in terms of | Coefficient of dispersion |
|---|---|
| Range | C.D. = (Xmax – Xmin) ⁄ (Xmax + Xmin) |
| Quartile Deviation | C.D. = (Q3 – Q1) ⁄ (Q3 + Q1) |
| Standard Deviation (S.D.) | C.D. = S.D. ⁄ Mean |
| Mean Deviation | C.D. = Mean deviation/Average |
फैलाव का सापेक्ष माप
फैलाव के सापेक्ष माप का उपयोग दो या दो से अधिक डेटा सेटों के वितरण की तुलना करने के लिए किया जाता है। यह माप इकाइयों के बिना मूल्यों की तुलना करता है। सामान्य सापेक्ष फैलाव विधियों में शामिल हैं:
- रेंज का गुणांक
- गुणांक का परिवर्तन
- मानक विचलन का गुणांक
- चतुर्थक विचलन का गुणांक
- माध्य विचलन का गुणांक
फैलाव का गुणांक
जब दो श्रृंखलाओं की तुलना की जाती है, जो उनके औसत में व्यापक रूप से भिन्न होती हैं, तो फैलाव के गुणांक की गणना (फैलाव की माप के साथ) की जाती है। फैलाव गुणांक का उपयोग तब भी किया जाता है जब विभिन्न माप इकाइयों वाली दो श्रृंखलाओं की तुलना की जाती है। इसे सीडी के रूप में दर्शाया गया है
फैलाव के सामान्य गुणांक हैं:
| सीडी के संदर्भ में | फैलाव का गुणांक |
|---|---|
| श्रेणी | सीडी = (एक्स अधिकतम – एक्स मिनट ) ⁄ (एक्स अधिकतम + एक्स मिनट ) |
| चतुर्थक विचलन | सीडी = (क्यू3 – क्यू1) ⁄ (क्यू3 + क्यू1) |
| मानक विचलन (एसडी) | सीडी = एसडी ⁄ माध्य |
| औसत झुकाव | सीडी = माध्य विचलन/औसत |
तिरछापन और कुर्टोसिस
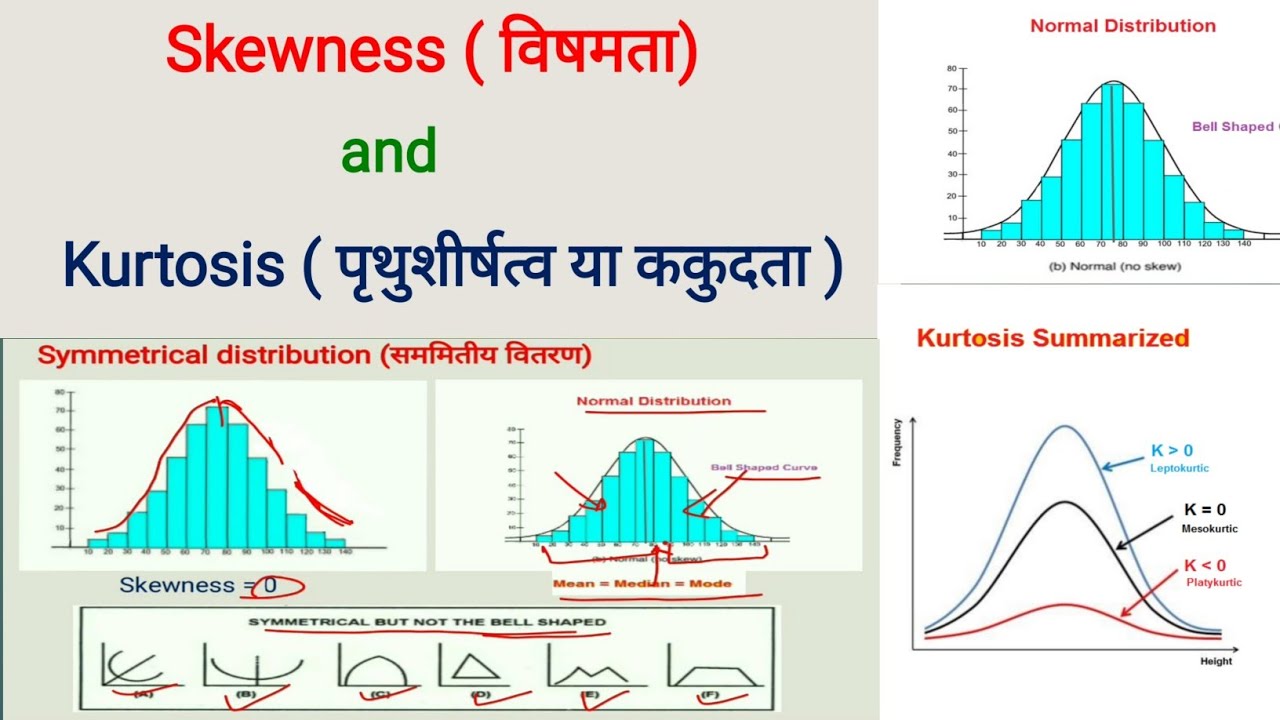
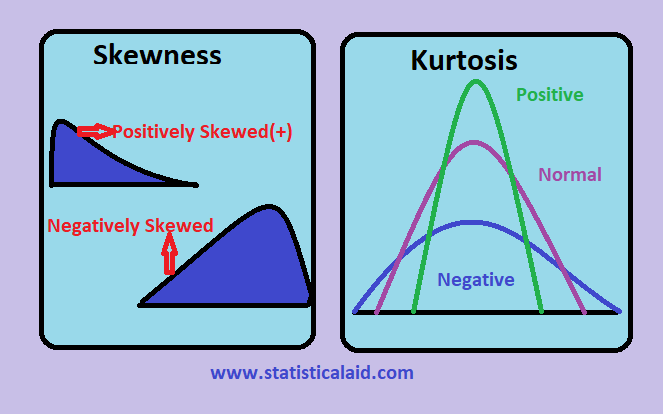
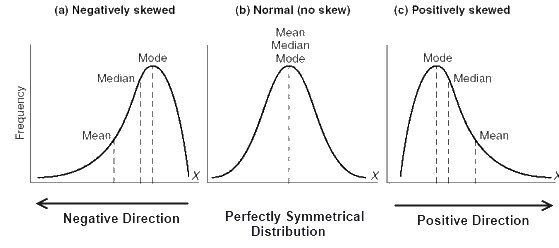
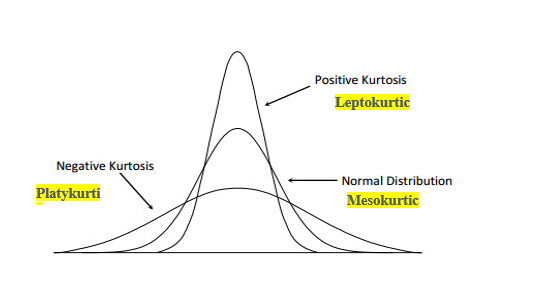
- Leptokurtic: तेजी से वसा पूंछ, और कम चर के साथ नुकीला।
- Mesokurtic: मध्यम शिखर
- Platykurtic: समतल चोटी और अत्यधिक फैलाव।
Module 3:
| correlation and regression correlation simple coefficient of correlation – karl pearson and rank correlation regression analysis estimation of regression line in a bivariate distribution least squares method |
सहसंबंध और प्रतिगमन सहसंबंध सरल सहसंबंध का गुणांक – कार्ल पियर्सन और रैंक सहसंबंध प्रतिगमन विश्लेषण द्विचर वितरण में प्रतिगमन रेखा का अनुमान न्यूनतम वर्ग विधि |
सहसंबंध और प्रतिगमन

कार्ल पियर्सन सहसंबंध गुणांक
कार्ल पियर्सन गुणांक को एक रैखिक सहसंबंध के रूप में परिभाषित किया गया है जो -1 से +1 की संख्यात्मक सीमा में आता है।यह एक मात्रात्मक विधि है जो X और Y चर के बीच रैखिक संबंध की तीव्रता बनाने के लिए संख्यात्मक मान प्रदान करती है।
सहसंबंध गुणांक को दो मात्रात्मक या गुणात्मक चर, यानी, एक्स और वाई के बीच संबंध के माप के रूप में परिभाषित किया जा सकता है। यह एक सांख्यिकीय उपकरण के रूप में कार्य करता है जो विश्लेषण करने में मदद करता है और बदले में, चर के बीच रैखिक संबंध की डिग्री को मापता है।
उदाहरण के लिए, किसी व्यक्ति की मासिक आय (X) में परिवर्तन से उनके मासिक व्यय (Y) में परिवर्तन होता है। सहसंबंध की सहायता से, आप उस डिग्री को माप सकते हैं जिस तक ऐसा परिवर्तन अन्य चरों को प्रभावित कर सकता है।
सहसंबंध गुणांक के प्रकार
चरों के बीच संबंध की दिशा के आधार पर, सहसंबंध तीन प्रकार के हो सकते हैं, अर्थात् –
-
सकारात्मक सहसंबंध (0 से +1)
-
नकारात्मक सहसंबंध (0 से -1)
-
शून्य सहसंबंध (0)
सकारात्मक सहसंबंध (0 से +1)
इस स्थिति में, X और Y के बीच परिवर्तन की दिशा समान है। उदाहरण के लिए, वर्कआउट की अवधि में वृद्धि से व्यक्ति द्वारा जलायी जाने वाली कैलोरी की संख्या में वृद्धि होती है।
नकारात्मक सहसंबंध (0 से -1)
यहां, X और Y वेरिएबल्स के बीच परिवर्तन की दिशा विपरीत है। उदाहरण के लिए, जब किसी वस्तु की कीमत बढ़ती है तो उसकी मांग कम हो जाती है।
शून्य सहसंबंध (0)
इस मामले में चरों के बीच कोई संबंध नहीं है। उदाहरण के लिए, ऊंचाई बढ़ने से किसी की बुद्धि पर कोई प्रभाव नहीं पड़ता है।
अब जब हमने इन बुनियादी बातों की अपनी याददाश्त को ताज़ा कर लिया है, तो आइए सहसंबंध के कार्ल पियर्सन गुणांक पर आगे बढ़ें।

Module 4:
| time series time series analysis concept and component determination of regular Trend and seasonal indices |
समय श्रृंखला समय श्रृंखला विश्लेषण अवधारणा और घटक नियमित रुझान और मौसमी सूचकांकों का निर्धारण |
समय श्रृंखला
समय श्रृंखला पूर्वानुमान पहले देखे गए मूल्यों के आधार पर भविष्य के मूल्यों की भविष्यवाणी करने के लिए एक मॉडल का उपयोग है
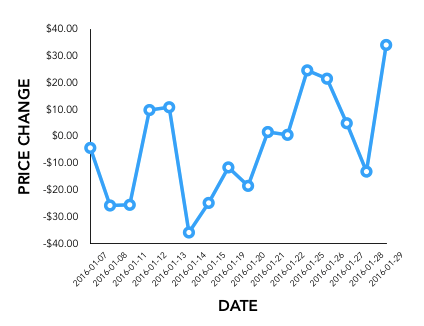
काल श्रेणी के अंग
(Components of Time Series)
1.दीर्घकालीन प्रवृत्ति या अपनति (Secular Trend or Trend)
लंबी अवधि में किसी श्रेणी के बढ़ने या घटने की सामान्य मूलभूत प्रवृत्ति को दीर्घकालीन प्रवृत्ति या उपनति कहते है।
2.आतर्व परिवर्तन या मौसमी परिवर्तन (Seasonal variations )
काल-श्रेणी में एक ही वर्ष में होने वाले नियमित अल्पकालीन उतार-चढ़ाव को मौसमी परिवर्तन कहते है।
3.चक्रीय उच्चावचन (Cyclical Fluctuations)
जब काल-श्रेणी में दीर्घकालीन नियमित उतार-चढ़ाव आते है तो वे चक्रीय उच्चावचन होते है, इन्हे व्यावसायिक चक्र (business cyclies) भी कहते है।
4.अनियमित या दैव परिवर्तन (Irregular or Random Variations)
जब आकस्मिक कारणों से अनियमित उतार-चढ़ाव आते है तो उसे क्रमहीन या अनियमित या दैव परिवर्तन कहते है। जैसे – भूकम्प, बाढ़, युद्ध, औद्योगिक संघर्ष आदि के कारण उतार-चढ़ाव। इनका पूर्वानुमान लगाना असंभव है।
दीर्घकालीन प्रवृति का मापन (Measurement of trend)
. स्वतंत्र हस्तवक्र या बिन्दुरेखीय रीति (Freehand curve of Graphic method)
काल-श्रेणी को बिन्दुरे-रेखीय पत्र पर अंकित करके कालिक-चित्र बनाया जाता है। बिन्दुओं के उतार-चढ़ाव को ध्यान में रखते एक वक्र खींचा जाता है, जो उच्चावचनों के मध्य से गुजरता है। इससे अल्पकालिक उतार-चढ़ाव दूर होकर काल-समंकों की दीर्घकालीन प्रवृत्ति प्राप्त होती है।
इस रीति में किसी प्रकार के गणितीय सूत्र की आवश्यकता न होने के कारण यह समझने में सरल एवं आसान है। इस रीति के द्वारा कोई निश्चित निष्कर्ष नहीं निकाला जा सकता है।
2. अर्द्ध-माध्य रीति (Semi-Average Method) –
इस रीति में समंक माला को दो समान भागों में बाँट लिया जाता है। विषम अंकों की स्थिति में बीच के अंक को छोड़कर समंक माला को दो समान भागों में बाँट लिया जाता है। दोनों समांतर माध्यों को बिन्दुरेखीय पत्र पर प्रांकित करके मिला दिया जाता है। यह रेखा दीर्घकालीन प्रवृत्ति को प्रकट करती है ।
इस रीति का प्रयोग केवल समंकों की दीर्घकालीन प्रवृत्ति रेखीय या लगभग रेखीय होने पर किया जाता है।
3. चल-माध्य रीति (Moving Average Method)
चल माध्य रीति में अनेक माध्य होते है । चल-इस की गणना करते समय सर्वप्रथम यह निश्चित करना होता है कि कितने वर्षीय माध्य निकलना है अर्थात तीन वर्षीय, चार वर्षीय, पाँच वर्षीय या सात वर्षीय आदि। इससे संबंधित कोई विशेष नियम नहीं है। तीन वर्षीय चल माध्य की गणना हेतु प्रथम तीन पक्षों का योग करके उसे दूसरे पद के सामने रखकर अगले स्तम्भ में उसे तीन से विभाजित करके रखा जायेगा। द्वितीय चल माध्य के लिए प्रथम पद को छोड़कर तीन पदों का योग किया जायेगा तथा पुनः उसी प्रक्रिया का अनुसरण किया जायेगा।
चल-माध्य विधि लोचदार (flexible) है, इस विधि के द्वारा लगभग सभी प्रकार के नियमित व अनियमित अल्पकालिक उच्चारणों का निर्गमन (Elimination) हो जाता है।
4. न्यूनतम वर्ग रीति (Method of Least Squares)
दीर्घकालीन प्रवृत्ति माप की यह सर्वोत्तम रीति है। इस रीति में बीजगणित पर आधारित सूत्र से एक रेखा का निर्माण किया जाता है, जो समंकमाला आधारित सूत्र से एक रेखा का निर्माण किया जाता है, जो समंकमाला की दीर्घकालीन प्रवृत्ति को प्रकट करती है। इस रेखा को सर्वाधिक उपयुक्तता की रेखा (Line of best fit) कहते है ।
5. अर्द्ध-लघुगणकीय या घातांकीय वक्र (Semi logarithmic of Expontial curve)
जब काल- श्रेणी में एक स्थिर प्रतिशत की वृद्धि या कमी हो हो अर्द्ध लघुगणितीय या घातांकीय वक्र का उपयोग किया जाता है।
समीकरण :- Log y = Log a + x Log b
मौसमी परिवर्तन मापन की विधि (Measurement of Seasonal Variations)
1. आर्तव मध्यक रीति (Seasonal average method)
इसका प्रयोग बारह-मासिक समंकों में ऋतुनिष्ठता का मापन करने के लिए किया जाता है। इसमें प्रत्येक माह के मूल्यों को जोड़कर 12 का भाग देकर मासिक आर्तव माध्य ज्ञात किया जाता है। बारह माह के मासिक आर्तव माध्य को जोड़कर 12 का भाग देकर सामान्य माध्य ज्ञात किया जाता है। सामान्य माध्य को 100 मानकर प्रत्येक मध्यक आर्तव को निम्न सूत्र द्वारा सूचकांक में परिवर्तित किया जाता है।
आर्तव विचरण सूचकांक = आर्तव माध्य / सामान्य माध्य * 100
2. प्रवृत्ति-अनुपात विधि (Ratio-to- Trend Method)
इसमें न्यूनतम वर्ग रीति द्वारा मौसमी अवधि की दीर्घकालीन उपनति ज्ञात की जाती है। यह विधि न्यादर्श पर आधारित है, इसकी गणन-क्रिया जटिल होता है।
सभी प्रवृत्ति अनुपातों का समान्तर माध्य ज्ञात करके सभी प्रवृत्ति-अनुपातों को आर्तव सूचकांक में बदलकर उनका सामान्य माध्य ज्ञात किया जायेगा। सामान्य माध्य को आधार (100) मानकर प्रवृत्ति माध्यों को आर्तव सूचकांक में बदला जायेगा।
प्रवृति अनुपात = मूल समंक / प्रवृति मूल्य * 100
3. चल-माध्य अनुपात विधि (Ratio-to-Moving Average Method)
इसमें बारह मासिक या चार त्रैमासिक चल-माध्य ज्ञात किये जाते है। सभी चल-माध्य अनुपातों का समांतर माध्य ज्ञात करके आर्तव विचरणों के सामान्य माध्य को आधार (100) मानकर सभी काल अवधियों के लिए आर्तव-सूचकांक तैयार किए जाते हैं।
4. श्रृंखला मूल्यानुपात विधि (Link Relative Method)
यह आर्तव वितरण की संतोषजनक परन्तु जटिल विधि है।
Module 5:
| index number concept price relative quantitative relative value relative lasperyers & Fisher Family budget method problem in the construction and limitation of number test for index ideal index number |
क्रमांक संख्या/सूचकांक संख्या अवधारणा कीमत सापेक्ष मात्रात्मक सापेक्ष मूल्य सापेक्ष लेस्परियर्स और फिशर परिवार बजट पद्धति निर्माण में समस्या एवं संख्या की सीमा सूचकांक के लिए परीक्षण आदर्श सूचकांक संख्या |
सूचकांक संख्या
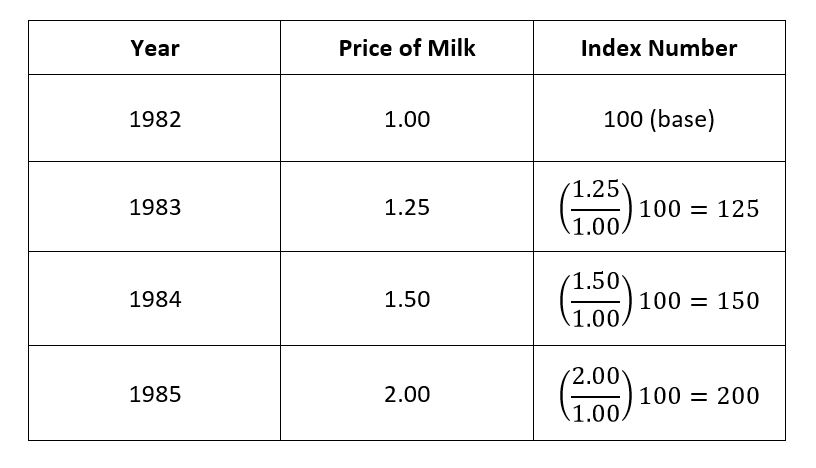
सूचकांक संख्या एक सांख्यिकीय उपकरण है जिसका उपयोग अर्थशास्त्र और व्यवसाय में भौगोलिक स्थानों, समय या अन्य पहलुओं से संबंधित व्यक्तिगत चर या चर के समूह में परिवर्तन को मापने के लिए किया जाता है। इस सांख्यिकीय उपाय का प्राथमिक उद्देश्य जटिल तुलनाओं को सरल बनाना है।
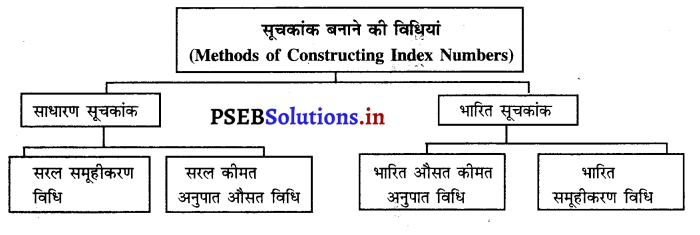
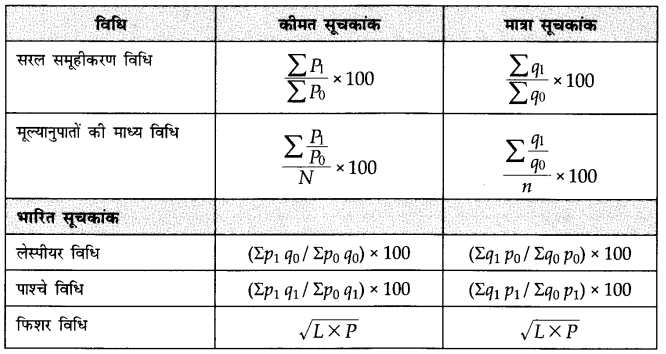
| लासपेरे की विधि | आधार वर्ष की मात्रा |
| पाशे की विधि | चालू वर्ष की मात्रा |
| फिशर विधि | अंतर्गत पाशे और लास्पेयर की संयुक्त तकनीकों |
P = Price Index of the current year
p0 = Price of goods at base year
p1 = Price of goods in the current year
q0 = Quantity of goods at base year
q1 = Quantity of goods in the current
पी = चालू वर्ष का मूल्य सूचकांक
p0 = आधार वर्ष पर माल की कीमत
p1 = चालू वर्ष में माल की कीमत
q0 = आधार वर्ष पर माल की मात्रा
q1 = वर्तमान में माल की मात्रा

टाइम रिवर्सल टेस्ट: (टीआरटी) : इस परीक्षण के लिए आवश्यक है कि कारक 100 को छोड़कर, पीछे की ओर गणना की गई सूचकांक संख्या आगे की गणना की गई सूचकांक संख्या का व्युत्क्रम होनी चाहिए। यानी पी 01 = 1 पी 10 1 पी 10 या पी 01 × पी 10 = 1 (गुणांक 100 को छोड़कर) कारक उत्क्रमण परीक्षण:- इस परीक्षण के लिए आवश्यक है कि मूल्य सूचकांक संख्या और मात्रा सूचकांक संख्या का उत्पाद कारक 100 को छोड़कर दो अवधियों के बीच होने वाले मूल्य में शुद्ध परिवर्तन के बराबर होना चाहिए। यानी पी 01 × क्यू 01 = ∑ पी 1 क्यू 1 ∑ पी 0 क्यू 0 ∑ पी 1 क्यू 1 ∑ पी 0 क्यू 0 = वी 01 (कारक 100 को छोड़कर)।
बिल्कुल! यहाँ TMBU (Tilka Manjhi Bhagalpur University) के B.A. Part‑III, Paper‑VI: QUANTITATIVE TECHNIQUES (मात्रात्मक तकनीकें) के लिए लेखांकन संक्षिप्त नोट्स दिए गए हैं, जो जल्दी रिविज़न और परीक्षा की तैयारी के लिए उपयोगी हैं:
📌 1. संख्यात्मक विधियाँ (Statistical Techniques)
1.1 औसत (Mean)
- साधारण माध्य (Arithmetic Mean, AM):
xˉ=∑xin\bar{x} = \frac{\sum x_i}{n} - वर्गित डेटा के लिए:
xˉ=∑fixi∑fi\bar{x} = \frac{\sum f_i x_i}{\sum f_i} - गुणोत्तर माध्य (Geometric Mean, GM):
GM=(∏xi)1/nGM = (\prod x_i)^{1/n} - हार्मोनिक माध्य (Harmonic Mean, HM):
HM=n∑1/xiHM = \frac{n}{\sum 1/x_i}
1.2 माध्य विचलन (Measures of Dispersion)
- परिसीमन (Range): maxx−minx\max x – \min x
- औसत विचलन (Mean Deviation):
MD=∑∣xi−xˉ∣nMD = \frac{\sum |x_i – \bar{x}|}{n} - वर्गमूल माध्य विचलन (Standard Deviation, SD):
σ=∑(xi−xˉ)2n\sigma = \sqrt{\frac{\sum (x_i- \bar{x})^2}{n}} - परसेंटाइल, क्वारटाइल, इत्यादि:
Q1 (25%), Q2 (Median), Q3 (75%)
1.3 सहसंबंध और प्रतिगमन (Correlation & Regression)
- सहसंबंध गुणांक (Correlation Coefficient, r):
r=∑(xi−xˉ)(yi−yˉ)∑(xi−xˉ)2∑(yi−yˉ)2r = \frac{\sum (x_i- \bar{x})(y_i-\bar{y})}{\sqrt{\sum (x_i- \bar{x})^2 \sum (y_i-\bar{y})^2}}
रंग: +1 से –1 - प्रतिगमन रेखा (Regression Line):
- YY पर XX की रेखा:
y−yˉ=byx(x−xˉ)y – \bar{y} = b_{yx}(x – \bar{x})
जहाँ byx=∑(xi−xˉ)(yi−yˉ)∑(xi−xˉ)2b_{yx} = \frac{\sum (x_i- \bar{x})(y_i-\bar{y})}{\sum (x_i-\bar{x})^2} - समरूप रूप से XX पर YY की रेखा तैयार
- YY पर XX की रेखा:
📐 2. वस्तु नाभिक (Index Numbers)
- आधार वर्ष (Base Year) व वर्तमान वर्ष (Current Year) में मूल्यों की तुलना
- सूची बनाने के प्रकार:
- लास्से पैस्ले (Laspeyres): ∑ptq0∑p0q0×100\frac{\sum p_t q_0}{\sum p_0 q_0} \times 100
- पास्चे (Paasche): ∑ptqt∑p0qt×100\frac{\sum p_t q_t}{\sum p_0 q_t} \times 100
- फिशर (Fisher): L×P\sqrt{L \times P} (लस्से × पास्चे)
🧮 3. समय-श्रृंखला विधियाँ (Time Series Methods)
- घटक: प्रवृत्ति (Trend), मौसमी (Seasonal), चक्रीय (Cyclical), अनियमित (Irregular)
- प्रवृत्ति विधियाँ:
- प्रत्यक्ष अनुमान
- साधारण रेखीय प्रतिगमन:
Tt=a+btT_t = a + bt - चलित माध्य (Moving Averages): 3, 5, 7-अवधि का
🧮 4. संभावना (Probability Basics)
- संख्या सिद्धांत (Probability Theory):
- प्रायोगिक / समीकरणीय प्रायिकता
- संयोगी घटनाएँ:
- संयुक्त (Joint Events) और स्वतंत्र तत्त्व (Independent Events)
🧾 5. आर्थिक अनुप्रयोग (Economic Applications)
- अनलटिडर और मांग‑आपूर्ति विश्लेषण
- गणितीय प्रतिरोधात्मक मॉडल, उपयोगकर्ता निर्णय‑ग्राफ़
- स्थिरता और समाश्छादन (Equilibrium)
📈 6. उपलब्ध व्यक्ति (Useful Formulae Summary)
| Topic | Key Formula |
|---|---|
| Arithmetic Mean | xˉ=∑xin\bar{x} = \frac{\sum x_i}{n} |
| Standard Deviation | σ=∑(xi−xˉ)2n\sigma = \sqrt{\frac{\sum (x_i – \bar{x})^2}{n}} |
| Correlation Coefficient | r=SxySxxSyyr = \frac{S_{xy}}{\sqrt{S_{xx}S_{yy}}} |
| Regression Coefficient | b=SxySxxb = \frac{S_{xy}}{S_{xx}} |
| Laspeyres Index | ∑ptq0∑p0q0×100\frac{\sum p_t q_0}{\sum p_0 q_0} \times 100 |
| Linear Trend | Tt=a+btT_t = a + bt |
⏱️ Examination Strategies
- फॉर्मूला याद रखें (+ small derivation समझें)
- ग्राफ़ खींचना अभ्यास करें (Regression line, Time‑series)
- वास्तविक अर्थ छात्रों को समझाने हेतु उदाहरण दें
- वस्तु‑विशिष्ट प्रश्न → जल्दी लिखें, वजह दें
📥 यदि आप चाहें तो:
- PDF संक्षेप ड्राफ्ट
- फॉर्मूला की आसान याद रखने वाली ट्रिक्स
- पेपरेबल सवालों की सूची
- पिछले वर्ष के प्रश्नों की सूची
बस बताइए, और मैं आपको यहां भेज सकता हूँ — फैट रिविजन ज़रूर हो जाएगा!
